
La escuela pitagórica en el siglo IV a. C surgió como una secta que planteaba el estudio de la religión y la ciencia por medio de los números, pero con un estricto sentido místico, y con enseñanzas que posteriormente se transmitieron de la boca de Anaximandro, en la búsqueda de lo “ilimitado.
Todos estos conocimientos encontraron eco en otras disciplinas que aplicaron los principios de las matemáticas, idealizadas por medio de la geometría, en tres figuras básicas: El círculo, como expresión de lo divino; el cuadrado, como representación de la Tierra, y el triángulo, como principio de manifestación. Estos trazos fueron parte de una ciencia contemplativa que representa las leyes de la naturaleza de todas las cosas que emanan de lo de arriba hacia abajo y que aplican de abajo hacia arriba.
Leonardo da Vinci, al inicio del renacimiento, pudo conceptualizar y plasmar en su obra el Hombre de Vitruvio, y dejar constancia de las proporciones ideales del cuerpo humano, que no solo representa lo físico, sino también todo el universo. De ello se extrajeron conceptos como la cuadratura del círculo o ad quadratum; abstracción filosófica, de la paradoja entre la proporción de lo divino con lo terreno, y del cual surge el concepto tanto de Pi (∏) 3.1416, y de Phi, como el número dorado 1.61, y que se refiere a una proporción o razón de un número irracional obtenida por el escultor griego Fidias, que representa la proporción fractal de todas las figuras geométricas de la naturaleza, utilizada en una multitud de proporciones y diseño de la arquitectura antigua.
Así aplicamos que todo lo que está manifestado en la creación sigue el mismo patrón de la creación de la forma, de la cual nacen las unidades de medida como herramienta del desarrollo de la humanidad.
Los egipcios fueron los primeros en otorgar este marco comparativo de medida, utilizando la distancia entre la palma y el codo, que establece antropológicamente un marco de referencia o proporción entre el hombre y el universo.
Estas medidas fueron la base de la mayor parte de las referencias de la Babilonia de Ezequiel, o el Israel de Salomón, en correspondencia con el Tabernáculo de Moisés y el Arca de la Alianza. El “codo real”, y el metro se basan en una vara de madera con marcas que representan 0.5236 m, que equivale a la sexta parte de Pi (3.1416/6= 0.52), y a Phi2 /5 = 2.6180/5 = 0.5236.

Si la antropometría nos comparaba con el universo conocido y el desconocido del cosmos, las edificaciones tendrían que establecer un intento por realizar cálculos como la distancia de la Tierra con la Luna, como es el caso de la Pirámide de Giza, con sus 218 metros, que se alza hacia los cielos como un monumento espectacular, que pretende describir la proporción de esa distancia que hoy sabemos que es de 384,400 km, cuyos cálculos se obtienen mediante el trazado de un círculo, un cuadrado y dos triángulos.
Por lo tanto, todo concepto filosófico tenía siempre una connotación mística, que ahora se explica perfectamente, de manera quizá coincidente, pero aplica perfectamente para entender la fisiología y la dinámica de la raíz de la aorta ante la presencia de aneurismas de la aorta ascendente, asociadas a insuficiencia aórtica.
Una comparativa casual es la simbología que rodea el saludo de namasté o námaster, que proviene de la palabra sanscrita hindú que demarca cortesía y/o reverencia: “Me inclino ante ti y te saludo”, “Lo divino dentro de mí te saluda. Este mudra, que hace que ambas palmas de las manos se una enfrente del pecho, justamente en el área del corazón, cuya disposición hace que los codos formen una escuadra, lo cual recuerda inmediatamente los cálculos geométricos necesarios para la generación de una estrategia para reparar la válvula aórtica con o sin remplazo de la aorta ascendente, con el objetivo de evitar la anticoagulación, además de la durabilidad y el periodo libre de enfermedad.
Nuevamente encontramos correlación entre el círculo que describe el anillo aórtico, la porción sinotubular (unión entre los senos de Valsalva y la aorta ascendente), tamaño de los senos de Valsalva, y el triángulo que describe dos catetos y una hipotenusa, todos relacionados con la longitud de la válvula, la altura de las valvas y el área de coaptación de las mismas, donde se aplica el teorema de Pitágoras, para este planteamiento de proporción geométrica.
La geometría es la base del estudio de la raíz de la aorta, pues el incremento del diámetro del anillo aórtico (distancia entre los dos codos: cateto b), puede ocasionar la separación de las valvas de la aorta, reduciendo la superficie de coaptación, y la unión de las valvas (unión de las palmas de las manos). Al realizar un análisis de los parámetros utilizados actualmente para medir la longitud geométrica (hipotenusa: c, la altura geométrica (cateto a), y el área de coaptación, en proporción con el diámetro del anillo aórtico y el número de valvas que tiene la válvula aortica.
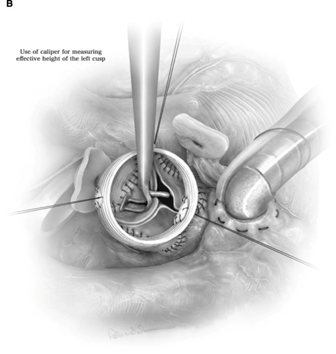
Este conocimiento aplica contundentemente a los principios básicos de la cirugía conservadora de la válvula aórtica, y mi filosofía personal de intentar, en la medida de lo posible, la anticoagulación, ya sea en pacientes jóvenes o en pacientes en la sexta década de la vida, de la cual tenemos hoy en día la capacidad de decidir objetivamente una estrategia de reparación, ya sea por una técnica de Yacoub o de David, con la ayuda del calibrador del Profesor Hans-Joachim Schäfers.
[1] https://midebien.com/los-origenes-de-la-calibracion/
[2] https://www.pngegg.com/es/png-clmij








